Quand des états exotiques de la matière aident à comprendre un précurseur d’El Nino

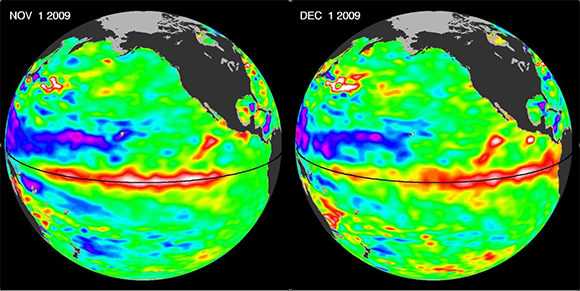
Les ondes équatoriales atmosphériques et océaniques correspondent à des anomalies de température qui se propagent le long de l’équateur à l’échelle planétaire. Certaines de ces ondes ne peuvent se propager que d’ouest en est. C’est le cas des ondes de Kelvin, observées notamment dans le Pacifique et identifiées comme un des précurseurs du phénomène El Nino. Ces ondes unidirectionnelles ont été découvertes dans les années 1960, mais leur origine physique restait jusque-là mystérieuse. En utilisant des outils de topologie développés ces dernières années dans un tout autre domaine de la physique, la matière condensée, des physiciens du Laboratoire de physique de l’ENS de Lyon (CNRS/ENS Lyon/Univ. Lyon 1) et du département de physique de l’université de Brown ont expliqué l’origine et la robustesse de ces ondes unidirectionnelles, piégées à l’équateur. Ils ont ainsi mis en évidence une analogie inattendue entre ondes géophysiques et ondes électroniques. Ce travail a été publié dans la revue Science.

La topologie permet de classer les objets selon la possibilité que l’on a de passer de l’un à l’autre de façon continue. Ainsi, une tasse à café et un donut appartiennent à la même classe topologique car l’on peut déformer continument la tasse à café jusqu’à former un donut. Les deux ont en effet un seul trou (l’anse de la tasse, le trou central du donut). Tandis que l’on ne pourrait pas déformer un croissant pour former un donut par exemple, car il faudrait creuser un trou dans le croissant, donc créer une discontinuité. La topologie permet aussi de classer des objets plus abstraits comme des familles d’ondes se propageant dans un matériau donné. Les propriétés topologiques ne décrivent dans ce cas plus l’existence de trous dans le matériau, mais de singularités dans cet ensemble d’ondes. Les physiciens de la matière condensée ont relié les propriétés remarquables de matériaux exotiques, isolants en volume mais très bon conducteurs électriques aux bords à l’existence de singularités dans ces familles d’ondes (l’équivalent des trous dans l’exemple de la tasse et du donut). Ils ont établi une correspondance entre le nombre de ces singularités et le nombre d’états unidirectionnels se propageant sans dissipation le long des bords de ces matériaux. La nature topologique de ces ondes confère aux matériaux des propriétés de conduction de bord très robustes, qui ne varient pas d’un échantillon à l’autre, de la même manière que le nombre de trous ne varie pas lorsque l’on passe de la tasse au donut. De même que la topologie explique l’émergence d’ondes électroniques piégées aux bords de ces matériaux, les physiciens ont montré qu’elle explique l’existence d’ondes unidirectionnelles dans l’atmosphère et l’océan, qui se comportent comme les ondes de Kelvin piégées à l’équateur.

Pour mettre en évidence l’existence d’ondes géophysiques topologiques, il a fallu dans un premier temps chercher des systèmes physiques fluides présentant les ingrédients minimaux pour l’observation d’ondes de bords unidirectionnelles. Le choix s’est porté sur une fine couche de fluide entourant une sphère en rotation, modèle couramment utilisé pour décrire la dynamique de l’atmosphère ou des océans. Ce système possède les ingrédients essentiels à l’apparition d’ondes topologiques grâce au double rôle joué par la force de Coriolis. D’une part, elle brise la symétrie par renversement du temps. Or, dans le contexte des isolants topologiques, il y a de fortes chances de voir apparaître des ondes avec des propriétés topologiques particulières si l’on brise cette symétrie temporelle. D’autre part, la force de Coriolis change de signe à l’équateur, lui faisant ainsi jouer le rôle d’une interface analogue au bord d’un isolant topologique.

Les chercheurs ont ensuite calculé un invariant topologique (l’équivalent du nombre de trous dans notre exemple « tasse-donut ») pour les familles d’ondes du modèle fluide. Ici, l’invariant correspond au nombre de singularités dans cet ensemble d’ondes. Ils ont relié cet invariant au nombre d’états unidirectionnels observés à l’équateur (en l’occurrence 2), et réalisé des simulations numériques montrant la robustesse des ondes équatoriales en présence de topographie, qui était jusque-là vue comme une source de désordre dans le système.

Les recherches se poursuivent afin de déterminer quelles pourraient être les autres manifestations physiques dans les fluides de cette propriété topologique.

En savoir plus

Topological origin of Equatorial waves 
Pierre Delplace, J. B. Marston et Antoine Venaille 
Science (2017), doi:10.1126/science.aan8819 
Lire l’article sur la base d’archives ouvertes ArXiv

Informations complémentaires

Laboratoire de physique de l’ENS de Lyon (CNRS/ENS Lyon/Univ. Lyon 1)