Un pendule dans le vent, ça bouge énormément
Sous l'action du vent, un objet tel qu'un arbre ou un avion, peut être soumis à des évènements soudains et parfois dommageables dont l'origine n'est pas toujours clairement identifiée. En étudiant les transitions d'un simple pendule sous l'action d'un vent régulier, les chercheuses et les chercheurs démontrent qu'elles obéissent à une statistique de la famille des statistiques extrêmes, c'est-à-dire dues à des évènements rares mais intenses.
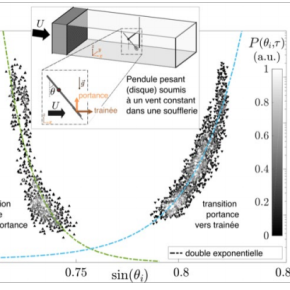
Un objet sous l'action du vent est soumis à des forces aérodynamiques qui sont la force de portance, celle qui fait voler les avions, et la force de trainée, qui caractérise la résistance de l'air. Des tourbillons apparaissent dans le sillage de l'objet, créant des fluctuations importantes de ces forces et pouvant générer des comportements soudains. Ainsi, un simple pendule circulaire soumis à un vent régulier possède deux positions stables en raison des équilibres entre son poids et les forces de portance et de trainée, mais subit des transitions soudaines entre ces deux positions en raison de leurs fluctuations1. En observant sur des temps longs le mouvement d’un tel pendule et en analysant ces transitions de façon statistique, les physiciennes et les physiciens ont montré que leur statistique était similaire à celle de la transition vers la turbulence observée dans le cas d'un fluide dans un tuyau, à savoir régies par des évènements rares et intenses. Ils posent ainsi le système canonique du pendule simple en interaction aérodynamique comme un paradigme étonnamment simple pour la compréhension des lois statistiques de phénomènes dits extrêmes. Ce travail a été effectué par des chercheurs du Laboratoire de physique (LPENSL, CNRS/ ENS Lyon) et publié dans les Physical Review Letters.
Pour réaliser cette étude, un système entièrement automatisé a été mis au point, afin de contrôler la position initiale du pendule, au choix sur l’une des deux branches stables (branche dominée par la portance ou branche dominée par la trainée) en fonction de la vitesse du vent, puis de détecter de manière systématique l’occurrence d’une transition d'une branche vers l’autre par un suivi précis de sa position angulaire, et enfin de ramener le pendule sur la branche initiale. En répétant un tel cycle des milliers de fois (ce qui correspond à plusieurs semaines d’expérimentation) il est possible de caractériser très précisément les lois statistiques régissant ces transitions. L’étude est particulièrement complexe car les transitions se produisent de manière aléatoire, avec des temps d’attente pouvant varier de quelques secondes à plusieurs heures. Grâce à cette observation, les chercheurs ont ensuite construit une modélisation des statistiques de transition du pendule à partir d’une analogie conceptuelle avec un grand problème de la mécanique des fluides : la transition vers la turbulence. De manière remarquable, il a été notamment observé que les fluctuations du couple exercé par les forces aérodynamiques sur le pendule obéissaient à une distribution de Gumbel, bien connue dans la famille des statistiques dites extrêmes. Cette étude indique aussi que les transitions observées sur le pendule ne sont pas déclenchées par des évènements exceptionnels provenant du vent appliqué mais auto-induites par des événements tourbillonnaires exceptionnels naissant dans son propre sillage. L'étape suivante est de visualiser le sillage du pendule de façon tridimensionnelle et résolue en temps, et d'utiliser ce système simple de pendule pour développer des protocoles de contrôle de sa position, avec de potentielles applications en aérodynamique où ces phénomènes de tourbillons de sillage sont bien connus.
Voir la vidéo sur la chaine du GDR Turbulence
Référence
Rare Event-Triggered Transitions in Aerodynamic Bifurcation. A. Gayout , M. Bourgoin et N. Plihon, Physical Review Letters. Publié le 9 mars 2021.
DOI : 10.1103/PhysRevLett.126.104501.
Article disponible sur les bases d’archives ouvertes hal et arXiv.