Un nouveau modèle de contagion sociale pour tenir compte des effets de groupe
Des modèles théoriques basés sur un réseau d'interactions entre personnes sont couramment utilisés pour décrire la propagation d'une maladie ou d'une idée dans une société. Pour aller plus loin dans la prédiction de cette propagation, des chercheurs ont développé un nouveau modèle de contagion qui prend en compte des interactions simultanées entre plusieurs personnes.
Les processus de contagion sont à la base de phénomènes d’importance considérable comme la propagation de maladies infectieuses ou celle d’opinions, d’informations et de rumeurs. Ces processus sont étudiés depuis longtemps afin de prédire leur impact dans une société. Les modèles théoriques de contagion simplifient la réalité et considèrent généralement comme élément de base des interactions entre deux personnes, l’ensemble de ces interactions constituant le réseau d’interactions dans la population. Par exemple, la propagation d’une maladie infectieuse comme la grippe est modélisée par le fait qu’un individu porteur de la maladie peut la transmettre à un individu sain lors d’un contact physique. Cependant, des interactions de groupe peuvent également jouer un rôle crucial : par exemple, il n’est pas équivalent de converser successivement avec deux amis ou ensemble avec les deux dans une discussion de groupe, où des effets d'entraînement peuvent jouer. C’est pour prendre en compte ces effets de groupe que, au sein d'une collaboration internationale, un chercheur du Centre de physique théorique à Marseille (CPT, CNRS/Aix-Marseille Université/Univ. Toulon) a proposé un nouveau modèle de contagion. Les chercheurs utilisent la notion mathématique de complexe simplicial, qui permet d’étendre le concept de réseau à des interactions de groupe : l’élément de base n’est plus uniquement une interaction entre deux personnes mais peut être une interaction entre un nombre arbitraire de personnes. Les auteurs ont ainsi pu montrer analytiquement et numériquement que les effets de groupe peuvent changer radicalement la dynamique du processus de propagation.
Dans un réseau, l’interaction entre deux personnes est représentée par un lien entre deux points. Dans le modèle développé ici, l’interaction entre deux personnes est généralisée à une interaction de groupe à l’aide d’objets mathématiques appelés simplexes, un simplexe étant un ensemble de n points permettant de décrire un groupe de n personnes (figure de gauche). Un complexe simplicial est un ensemble de simplexes reliés, ce qui est bien adapté pour décrire une structure de société où des interactions deux à deux coexistent avec des interactions de groupe impliquant plus de deux personnes. Contrairement au cas des réseaux pour lesquels la notion de groupe n'existe pas, on peut distinguer un ensemble de trois interactions deux à deux d’une interaction triple (figure du milieu). Dans le modèle proposé, la contagion d’une idée peut se produire aussi bien lors d’une interaction deux à deux que lors d’une interaction de groupe de n personnes dont (n-1) sont déjà convaincues de l’idée, avec des probabilités potentiellement différentes (figure de droite). La contagion d’une fraction de la population s’opère alors de manière beaucoup plus brutale et rapide qu’avec seulement des interactions entre paires. De plus, il existe une zone de paramètres où sont possibles aussi bien la propagation que la disparition de l’idée, en fonction des conditions initiales : ceci permet d’expliquer la nécessité d’une masse critique initiale de personnes convaincues pour qu’une idée se propage, comme cela a été montré empiriquement récemment.
Les chercheurs comptent maintenant étudier des données empiriques pour trouver des signatures validant leur modèle, et l’étendre à des processus de contagion de maladies infectieuses, pour lesquels l’impact de tels effets de groupe est encore inconnu.
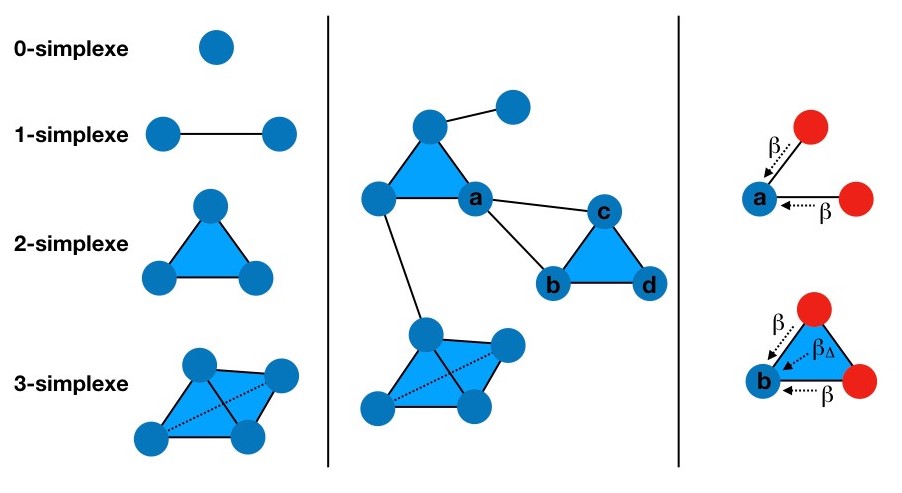
Au milieu : un exemple de complexe simplicial représentant une structure sociale où des interactions entre deux personnes coexistent avec des groupes plus importants. On distingue le triangle « creux » abc formé simplement de trois interactions à deux personnes (ab, bc et ca) et le triangle « plein » ou 2-simplexe bcd dans lequel les interactions bc, cd, bd sont complétées par l’interaction triple bcd.
A droite : les nœuds rouges représentent les individus déjà convaincus et les nœuds bleus ceux qui ne le sont pas encore ; dans la configuration du haut, le nœud bleu peut être convaincu par chacun de ses voisins avec une probabilité b par unité de temps ; dans la configuration du bas, à ces probabilités s’ajoute la probabilité bD par unité de temps d’être convaincu lors d’une interaction de groupe.
© CPT (CNRS/AMU/Univ. Toulon)
Référence
Simplicial models of social contagion, Iacopo Iacopini, Giovanni Petri, Alain Barrat et Vito Latora, Nature Communications, le 6 juin 2019. DOI: 10.1038/s41467-019-10431-6
L’article scientifique est disponible sur les bases d’archives ouvertes ArXiv et HAL